Research

Data models are central and used extensively in signal and image processing for various tasks. Such models impose a mathematical structure on the signals of interest in order to capture their true dimensionality, thereby enabling their effective processing. Choosing a well-fitted model for a source of interest is often key for leading to successful applications. Models play a key role in inverse problems (denoising, deblurring, super-resolution, inpainting, …), and in many other tasks (anomaly detection, segmentation, synthesis, …). A careful study of the vast literature in signal and image processing from the past several decades reveals a continuous evolution of signal modelling techniques, gradually leading to better performance in the applications they were brought to serve. In this respect, sparse representation has emerged in the last two decades as a leading, popular, and highly effective signal model. Competitive alternatives to is are the Gaussian Mixture Model (GMM) and its variants.

The sparse representation model describes a given signal x as a linear combination of few atoms from a pre-specified dictionary D. Put in algebraic terms, x is supposed to be equal to Da, where a is a sparse vector serving as the signal representation. A fundamental task in this model is known as “atom-decomposition”: given x and D, find the sparsest vector a to satisfy the equation x=Da. This problem is known to be NP-hard, and various approximation (also referred to as pursuit) algorithms were developed to solve it.

This description by itself may not seem ground-breaking, so what is it that makes this model so fascinating and appealing? The explanation is given by a blend of the following features: (i) the simplicity, elegance and intuitiveness of this model; (ii) the universality that makes this model capable of describing a variety of data sources, (iii) the emergence of exciting theoretical questions to which this model leads; and (iv) the existence of a clear path from these theoretical questions (and the answers given to them), to successful algorithms and applications.

This model, and a variety of its flavors, has been the focus of many of our papers, exploring numerical pursuit algorithms for approximating the representation, studying the core properties of this model and evaluating theoretical performance guarantees of these pursuit methods, addressing ways to learn the dictionary D from examples, and using this model for handling applications in signal and image processing. Interestingly, the work on compressed-sensing (CS) has also contributed in a large part to the popularity of this model, as it added another layer of theory and practice to sparse representations, in the context of sampling. So strong was the impact of CS that many today identify the entire field of sparse representations with it.

If several layers of the above-described sparse representation model are chained together (i.e. the representations themselves have sparse decomposition), we get an interesting new model construction of great interest. On one hand, this new structure leads to a model that describes the same signal in several parallel ways, each given in a different abstraction level. As such, this model poses a stringer structure on the signals of interest, thus serving them better. More exciting is the fact that pursuit algorithms, designed to expose the signal representations, lead naturally to classic deep-learning architectures of various sorts (feed-forward, recurrent, …) . These can now be accompanied by a new ability of theoretically analyzing their performance bounds. The multi-layer sparse representation model is an exciting new front of research that could lead to a systematic construction of a comprehensive theory for deep-learning.

This is THE revolution of the last two decades, carrying in it a great potential for a disruptive burst of new technologies in artificial intelligence and closely related fields. What do I think of deep learning is general, and how does this field interface with my work in signal and image processing? I recommend that you read this article, which I published in SIAM News in May 2017.

My own work in this arena is theoretically oriented, trying to decipher the origins of the proposed architectures and algorithms, first in order to better motivate them, and later in order to improve them. In this context, the above-described multi-layered modeling approach seems a promising path and we have already several key results in this direction. In parallel, my team’s research is focusing on generative models for visual and auditory data, working on various asspects of Generative Adversarial Networks (GAN’s) and Diffusion Models. Most of our efforts in this front are geared towards using these techniques for addressing a modern solution of inverse problems by sampling from the posterior, instead of computing the MMSE solution.

Many problems in signal and image processing can be posed as the need to recover a signal from a corrupted version of it. In image processing, this breed of tasks includes cleaning of noise (denoising), deblurring, super-resolution, inpainting (filling in missing parts in an image), tomographic reconstruction, and more. Various techniques have been proposed over the years to tackle such problems, forming a rich and exciting field of research that stands in the intersection of signal and image processing, estimation theory, optimization, and applied mathematics. A common approach taken in formulating these recovery problems is a Bayesian point of view, in which the overall task becomes an energy minimization task. Another key ingredient in such methods is the prior distribution of the unknown, or in its deterministic view, the regularization scheme that stabilizes the degradation inversion. Many of our papers address inverse problems using these ingredients in various ways, adopting theoretic, numerical, and application points of view.

A modern view of inverse problems that fascinates me is the ability to model better the posterior and then offer fair samples from it. This changes the rules of the game, as it enables getting perfect perceptual quality results to inverse problems, while accompanying these with an uncertainty estimation. In this context, Conditional GANs and Diffusion Models are most appealing.

Image denoising is the simplest inverse problem, and by far, the most studied one. In its classical form, this problem addresses the desire to remove white additive Gaussian noise from an image, while preserving the image content as much as possible. Why is this problem so popular? Several explanations could be given:

• Denoising is an important and practical problem. If you do not believe this, simply go to your personal photo-album and zoom in on any arbitrary image – you are likely to see traces of noise there. The sensed images are typically noisy, and especially so in poor illumination conditions. Every digital camera includes some sort of a denoising algorithm in order to provide better looking results.
• Due to its simplicity, the denoising problem has been a convenient entry point to almost every mathematical idea that was brought to image processing. Estimation theory, Harmonic analysis and wavelets, Partial differential equations, Adaptive filters, Regularization theory, Optimization, Robust statistics, Sparse representations, Example-based regularization, and more, all made their first appearance in image processing by treating the image denoising problem.
• Recent work has shown that every inverse problem can be solved by a chain of denoising steps, and thus a good denoising algorithm is so much more than just noise cleaner. Another fascinating branch of recent work shows that denoisers could be the (sole!) engine behind the best available image synthesis methods — Diffusion Models.

Numerous algorithms have been proposed to solve this problem, and the recent ones from the last decade are performing amazingly well. These are led today by deep-learning based solutions. In fact, these recent algorithms perform so well that researchers, such as Peyman Milanfar, Anat Levin, and Boaz Nadler, started speculating whether we are touching the ceiling in terms of the achievable noise decay.

Many of our research projects touched on the denoising problems, which keeps puzzling us. We devised novel such methods for noise removal, we generalized them to other noise characteristics such as Poisson, we boosted existing methods’ performance by the SOS scheme, and more. More recently we have been deploying our denoisers to synthesize images using Denoising Diffusion Probabilistic Models (DDPM), and use this to offer alternative and far morew appealing solutions to general inverse problems.

The classic field of signal processing considers uniformly sampled signals given on a clear measurement grid. Modern data sources, on the other hand, often produce signals lacking such pleasant sampling format. Consider for example traffic load data gathered by thousands of sensors spread in critical junctions in a predefined geographic region, accumulated over time. These signals are far more complex to process, as most of the familiar tools in signal processing (such as filtering, Fourier transform, sampling theorems, and more) are rendered useless for them. Such signals can be modeled as residing on a graph, where the nodes represent the sensing points, the edges of the graph represent the distances between nodes, and the signal itself are scalar values populating each node. The field of graph signal processing aims to adapt the classic tools to such signals. Our own work on this subject started by extending the Wavelet transform to graphs signals, and our later focus was on the generalization of the sparse representation model to cope with these breed of signals.

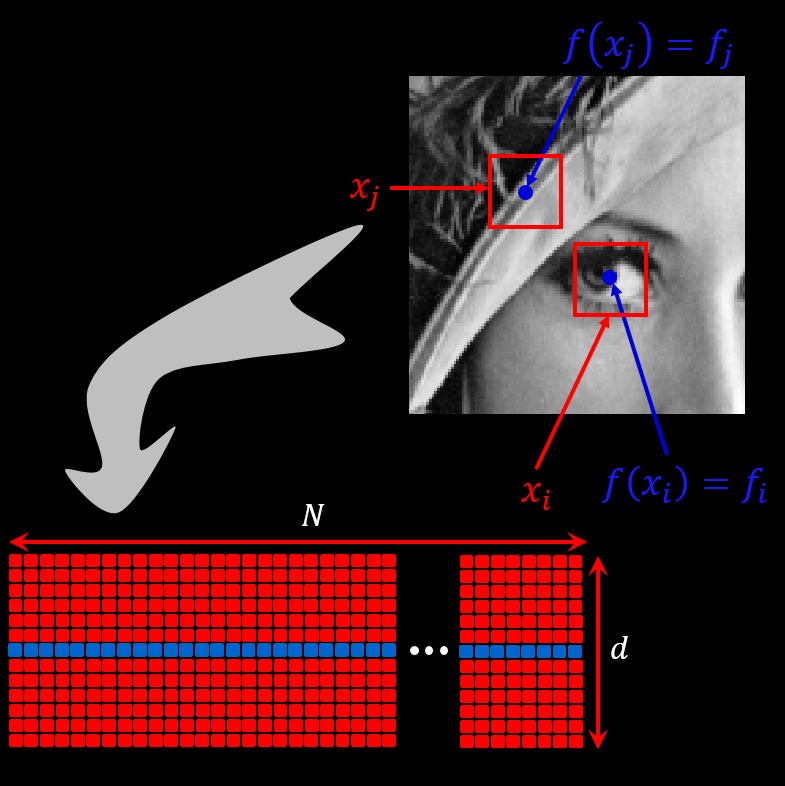
Imposing sophisticated models on full images is hard and even impossible due to the curse of dimensionality, and the difficulty to adapt such a global the model properly to the data. A technical remedy that we and many others adopted in the past decade is to operate locally on small fully overlapped patches, imposing the models on them independently, and then fusing their results to form the global image. Surprisingly, alongside the benefit of being much simpler, this strategy often leads to state-of-the-art results in inverse problems such as denoising, inpainting, super-resolution, deblurring, CT and MRI reconstruction, and more. How can this be explained? The bad news are that there is still no clear and final answer to this question. The good news, though, are that we are getting closer, with several identified key findings. We have defined the global model that stands behind this strategy, identified to be the Convolutional Sparse Coding model. We have managed to extend much of the known theory of sparse representation to this model while emphasizing local sparsity, and we have found effective ways to learn this model globally while operating only locally. We are struggling now to find ways to harness this global model successfully in inverse problems, in a way that could explain the above described success of the local strategy.

In the context of image processing, super-resolution is the process of taking a low-resolution input image(s) and producing a refined, better resolution, output image(s). There are two versions of this problem, and our group has studied both over the years:

• Single image super-resolution: In this problem we are given just one low-resolution image, and our goal is to enhance it to have better resolution, being able to see more refined details. This is clearly an impossible task if no additional information is given. And so, such algorithms typically rely on a model or on an external database of image examples to fulfill its goal.
• Multiple image super-resolution: In this form of the problem, we are given a set of images of the same object, and our goal is to fuse them to create a better looking result. In this case, the availability of several input images (taken at slightly different settings) creates a surprising opportunity to increase the output resolution, often times leading to fantastic results. Here as well, a model could support the recovery process, as indeed practice in many of exiting algorithms. Solving this problem is considered to be much harder than the single image one due to the involvement of fine registrations between the given images.

My first encounter with the topic of (multiple image) super-resolution was in 1991, when I saw the seminal paper by Irani and Peleg on this subject. I decided to make this my PhD work (1993-1996), and in fact, I never stopped working on this topic ever since. My research on super-resolution had several generations, the early one in my PhD and later with Payman Milanfar and Sina Farsiu considered the classic approach of registering, shifting, and then merging the images to form the outcome. The next generation, together with Matan Protter, consisted of a more robust treatment of the motion estimation by operating locally on patches. The more recent work with Yaniv Romano and Alon Brifman uses the Plug-and-Play-Prior and RED schemes in order to exploit available denoising algorithms to solve the super-resolution problem. I believe I am ready now to move to the next generation solution of super-resolution – stay tuned.